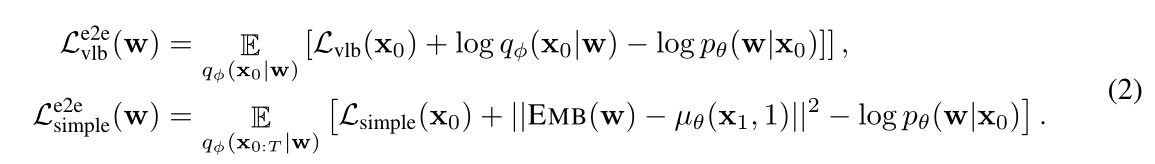Diffusion-LM Improves Controllable Text Generation
原文链接:Diffusion-LM Improves Controllable Text Generation
他人博客:
这可能会是我最像技术博客的一篇博客。
是一些下周组会要讲解的内容,但是自己其实对此也知之甚少,讲解前乃至到今天已经很紧张了,写一篇博客来明确一下自己的脉络。(顺便偷偷吐槽,扩散模型是非常数学的模型,但是自己的数学又很不行,感觉是在最紧张的时候给自己挖了一个最深的坑)
如果想说起Diffusion Model,我们要从所有的生成模型说起。
生成模型
目标
生成模型的目标是,给定训练数据,希望能获得与训练数据相同或者类似的新数据样本。举个栗子的话就是,在训练集当中给出一些🐎的照片,我们希望模型能够学习🐎的样子,从而产生看起来很像🐎的图像。(当然是不包含在训练集当中的)
从生成模型的目标当中我们可以很容易发现,我们要得到的是一个概率模型,因为每次生成模型要给出不同的🐎的图像,而不能每次都产生同一个图像。我们将产生的一系列图像(当然也不仅仅限于图像,文本等各个方面生成模型都有很广泛的应用)的概率分布记作$p(x)$。
常见的生成模型还是有很多的:GAN,VAE,Flow-based models(流模型,用的很少以至于都没听说过),Diffusion model.(扩散模型)
隐变量
对于许多许多不同的模态(图像,文本,音频等等),我们可以将可以观察到的真实的数据分布视为由相关的看不见的隐变量表示或生成,一般记作$z$.
看的博客/教程中举了一个例子,蝴蝶的颜色是由更细微的鳞片所标识出来的,我们希望能够通过颜色来反向推出鳞片的状态,这里鳞片大概就是$z$的意思。
VAE(Auto-encoding Variational Bayes)
讲到diffusion model,也就是扩散模型,我们很难不提到各种生成模型,而生成模型的老祖宗貌似就是AE模型,我们从老祖宗的儿子VAE开始说起。
Intuition
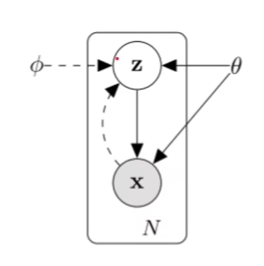
我们首先给定变量$x$,一般是比较高维度的变量,和隐变量$z$,假设当前的groundtruth(真实答案)为$\theta$。
我们假设$z$满足这样的分布$p_\theta(z)$,则有$p_\theta(x\mid{z})$
可以看到,我们想追求的目标是根据$x$和$\phi$来尝试求得$z$,以及可以通过$\theta$和$z$求得$x$。
还没写完,先写后面一点点的(因为发现换了个方式推导好像和VAE关系又小了那么一点点)
Diffusion Model
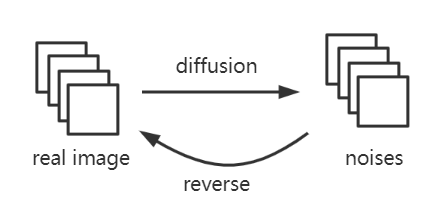
我们前面已经提到,Diffusion Model是一个生成模型,其目的是产生与训练数据类似的真实分布。对于扩散模型,其分为扩散过程和还原过程。
Model Process
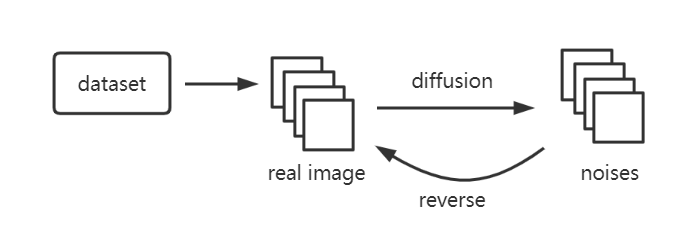
模型的整体流程大概如上所示,正常的diffusion过程以及反向的reverse过程。
在训练过程当中,从数据集当中拿出真实的图片,在去噪的过程当中衡量去噪后的图片和原图的差距。
这里可以使用机器学习当中的$l1\ loss/l2\ loss$来衡量。
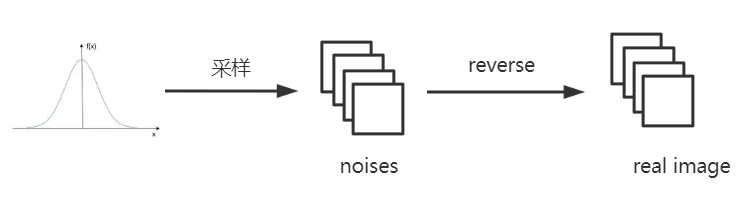
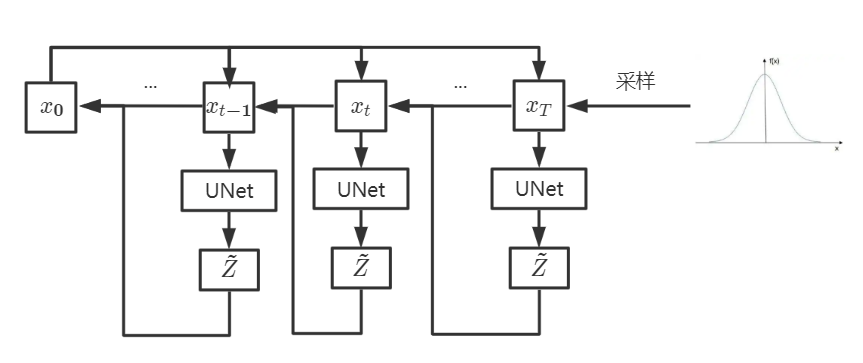
在重建过程当中,从高斯分布当中采样很多的噪声图,通过已经训练好的training phase的reverse阶段,来得到真实的图像显示。
Diffusion Phase
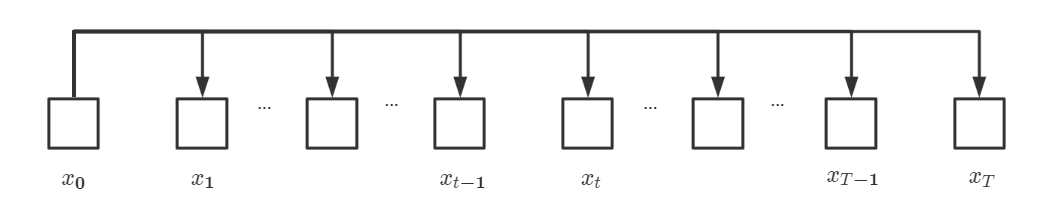
如前文所说明的,扩散过程是向原图像当中逐步添加高斯噪声的过程,我们可以将整个流程表现如下图所示:
单步扩散
我们所关注的是每一步逐渐添加高斯噪声的过程,给出每一步添加高斯噪声的公式:
\[x_t=\sqrt{1-\beta_t}x_{t-1}+\sqrt{\beta_t}Z_t,Z_t\sim{N(0,\textbf{I})}\]在添加高斯噪声的过程当中,每次向其中添加的高斯噪声的比例不同,由上式可得其由$\beta_t$决定。我们很容易能够有这样的直觉,每步向其中添加高斯噪声的比例是并不相同的,由于一开始的图像更加趋近于原图,我们稍微添加一点点高斯噪声就会能够对原先图像产生比较大的影响;而在比较靠后的添加高斯分布的过程当中,由于图像本身已经比较趋近于纯高斯噪声,我们势必向其中添加比较大比例的高斯噪声才会对图像产生比较明显的影响。
而且,对于整个的扩散步数$T$来说,我们需要保证最后的图像趋近于完全的高斯噪声,而不能包含原有的图像信息。因此这里在设置步数的时候也应该设置的比较大。
因此这里,在diffusion的过程当中,我们$\beta_t$是逐渐变大的,而在原文当中$\beta_t$是由$10^{-4}\to{2\times{10^{-2}}}$线性变化的。
多步扩散
我们在上节当中给出了每一步添加噪声的公式(1):
\[x_t=f(x_{t-1})=\sqrt{1-\beta_t}x_{t-1}+\sqrt{\beta_t}Z_t,Z_t\sim{N(0,\textbf{I})}\tag{1}\]有了一步扩散的公式,我们自然会想到,如果我们可以求得从$x_0$开始到$x_t$当中多步的扩散公式,就可以比较方便高效地训练模型,很自然的,我们可以递归的书写上面单步扩散的公式,但是这里论文聪明地做了一些处理,使得我们的计算和表示更加方便自然。
下面的内容包含大量的数学公式。
我们首先做一步换元,用$\alpha_t$来替代$1-\beta_t$,随后我们递归地书写单步扩散公式:
\[1-\beta_t=\alpha_t \tag{2}\] \[x_t=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}Z_t \tag{3}\] \[x_{t-1}=\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}Z_{t-1} \tag{4}\]我们随后将式(4)代入式(3)可得:
\[\begin {aligned} x_t &= \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}Z_{t-1})+\sqrt{1-\alpha_t}Z_t \\\ &=\sqrt{\alpha_{t}\alpha_{t-1}}x_{t-2}+\sqrt{\alpha_{t}-\alpha_{t}\alpha_{t-1}}Z_{t-1}+\sqrt{1-\alpha_t}Z_t \end {aligned} \tag{5}\]观察式(5),我们可以知道,$Z_{t-1},Z_{t}\sim{N(0,\textbf{I})}$,由此我们观察式(5)的后两项,其也是均值为0的高斯分布:$\sqrt{\alpha_{t}-\alpha_{t}\alpha_{t-1}}Z_{t-1}\sim{N}(0,\alpha_{t}-\alpha_{t}\alpha_{t-1}),\sqrt{1-\alpha_t}Z_t\sim{N}(0,1-\alpha_t)$。
由于高斯分布的可加性,我们可以很容易得到,后两项的和其也是均值为0的高斯分布:$Z’\sim(0,1-\alpha_{t}\alpha_{t-1})$,则式(5)可以写作式(6)的形式:
\[x_t=\sqrt{\alpha_{t}\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t}\alpha_{t-1}}Z,Z\sim{N}(0,\textbf{I}) \tag{6}\]观察从式(3)到式(6)的过程,我们由此可以递归地写出$x_t=f(x_0)$的表达式(7):
\[\begin {aligned} x_t&=\sqrt{\alpha_{t}\alpha_{t-1}...\alpha_2\alpha_1}x_{0}+\sqrt{1-\alpha_{t}\alpha_{t-1}...\alpha_2\alpha_1}Z,Z\sim{N}(0,\textbf{I}) \\\ &=\sqrt{\bar{\alpha_{t}}}x_{0}+\sqrt{1-\bar{\alpha_{t}}}Z,\bar{\alpha_t}=\prod_{i=1}^{T}{\alpha_i},Z\sim{N}(0,\textbf{I}) \end {aligned} \tag{7}\]至此,我们得到了从$x_0$一步扩散到$x_t$的公式,我们可以将diffusion过程转换为如下图所示。
Reverse Phase
在diffusion的过程当中,我们可以得到从$x_0$推导到$x_t$的过程,由此类似的,我们应该可以得到从$x_t$反推到$x_0$的公式,这里我们也很容易就可以给出这样的表达式(8):
\[x_0=\frac{1}{\sqrt{\bar{\alpha_{t}}}}(x_t-\sqrt{1-\bar{\alpha_{t}}}\tilde{Z}) \tag{8}\]在式(8)引领下,我们可以给出这样的训练过程:
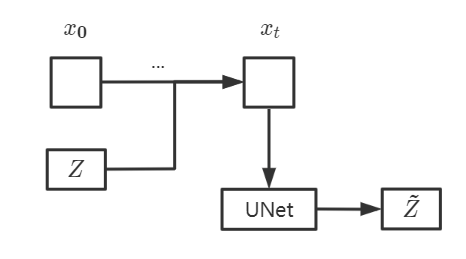
我们在这里首先由采样的噪声$Z$和原图像$x_0$,根据公式(7)推得$x_t$,再将$x_t$送入UNet网络当中,通过UNet去预测噪声$\tilde{Z}$,并且最终比较$Z$与$\tilde{Z}$,通过这样的方式完成训练。(需要注意的是,这里我们的输入除了$x_t$还有$t$,我们需要告诉UNet这是第几步去噪)
\[\tilde{Z}=UNet(x_t,t) \tag{9}\]从直觉上来讲,或者说显而易见的是,我们这样的训练过程得到的是一步reverse到$x_0$的过程,根据实际的实验结果显示,这样一步重建的过程并不是很清晰,效果不好。我们实际上的训练过程是采用一步步的reverse。
因此在这里,从后到前的,我们希望由第$t$步推导出第$t-1$步的噪声图像,从而步步推导至$x_0$。即,我们想要求得的是一个这样的表达式:
\[x_{t-1}=f(x_t,\tilde{Z})\]ps:这里给自己标注一点,以防止自己晕了,这里UNet所预测出的$\tilde{Z}$和公式(3)当中的$Z$显然不是一种东西,一个是从$t-1$推导到$t$的噪声,一个是从$x_0$推导到$x_t$的噪声(事实上是UNet预测的噪声),不可能直接通过公式3倒推的
根据上面的ps,我们发现,其实$x_{t-1}$是不容易直接求得的,我们这里求得的实际上是$q(x_{t-1}\mid{x_t})$的分布,随后通过重参数的方法在$q(x_{t-1}\mid{x_t})$当中采样得到一个$x_{t-1}$即可。这里采样的过程实际上是重参数化的过程,稍微偷懒一下粘贴一下别人的博客内容:
而对于$q(x_{t-1}\mid{x_t})$,这里我们是可以通过贝叶斯公式来进行转换,从而化为我们可求的分布的。
\[q(x_{t-1}\mid{x_t})=\frac{q(x_{t},{x_{t-1}})q(x_{t-1})}{q(x_{t})} \tag{10}\]而转换到这里,这些分布都是我们已知的,接下来的内容仍然包含很多数学推导。
ps:我们知道一个元素本身就等同于知道他的分布,因为他们都是从一个高斯分布当中采样得到的(当然,根据重参数化技巧,可以转换为从一个标准高斯分布当中采样)
\[x_t=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}Z_t\sim{N(\sqrt{\alpha_t}x_{t-1}, (1-\alpha_t)\textbf{I})}\] \[x_t=\sqrt{\bar{\alpha_t}}x_{0}+\sqrt{1-\bar{\alpha_t}}Z\sim{N(\sqrt{\bar{\alpha_t}}x_{0}, (1-\bar{\alpha_t})\textbf{I})}\] \[q(x_t\mid{x_{t-1}})\sim{N(\sqrt{\alpha_t}x_{t-1}, (1-\alpha_t)\textbf{I})}\] \[q(x_t)\sim{N(\sqrt{\bar{\alpha_t}}x_{0}, (1-\bar{\alpha_t})\textbf{I})}\] \[q(x_{t-1})\sim{N(\sqrt{\bar\alpha_{t-1}}x_{0}, (1-\bar\alpha_{t-1})\textbf{I})}\]ps:这里对于后三个式子,我个人认为写的不是很符合标准,但是大致的意思表示:左边的分布就是右边的高斯分布,两边的均值和方差完全相同(我只是对$\sim$符号的使用存疑)。
而我们此时想将这些高斯分布组合在一起,首先给出高斯分布的表达式(正态分布):
\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\propto\exp(-\frac{(x-\mu)^2}{2\sigma^2})\]因此式(10)正比于下式,由于我们所求的是$q(x_{t-1}\mid{x_t})$,其实我们更关注于$x_{t-1}$,我们可以对$x_{t-1}$展开并配方
\[\begin {aligned} \frac{q(x_{t},{x_{t-1}})q(x_{t-1})}{q(x_{t})}&\propto\exp(-\frac{1}{2}(\frac{(x_{t}-\sqrt{\alpha_{t}}x_{t-1})^2}{1-\alpha_{t}}+\frac{(x_{t-1}-\sqrt{\bar\alpha_{t-1}}x_{0})^2}{1-\bar\alpha_{t-1}}-\frac{(x_{t}-\sqrt{\bar\alpha_{t}}x_{0})^2}{1-\bar\alpha_{t}})) \\\ &\propto\exp(-\frac{1}{2}((\frac{\alpha_t}{1-\alpha_t}+\frac{1}{1-\bar\alpha_{t-1}})x_{t-1}^2-2(\frac{\sqrt{\alpha_t}x_t}{1-\alpha_t}+\frac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}})x_{t-1}+\frac{x_t^2}{1-\alpha_t}+\frac{\bar\alpha_{t-1}}{1-\bar\alpha_{t-1}}x_0^2-\frac{(x_{t}-\sqrt{\bar\alpha_{t}}x_{0})^2}{1-\bar\alpha_{t}})) \\\ &\propto\exp(-\frac{1}{2}((\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}})x_{t-1}^2-2(\frac{\sqrt{\alpha_t}x_t}{\beta_t}+\frac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}})x_{t-1}+C)) \end {aligned}\]我们将$x_{t-1}$视为主要变量,从而将原式整理为关于$x_{t-1}$的二次项:
\[\begin {aligned} \frac{q(x_{t},{x_{t-1}})q(x_{t-1})}{q(x_{t})}&\propto\exp(-\frac{1}{2}(Ax_{t-1}^2+Bx_{t-1}+C)) \\\ &\propto\exp(-\frac{1}{2}A(x_{t-1}+\frac{B}{2A})^2-\frac{1}{2}(C-\frac{B^2}{4A})) \\\ &\propto\exp(-\frac{1}{2}A(x_{t-1}+\frac{B}{2A})^2+D) \end {aligned} \tag{11}\]对于式(11)的$D$部分,由于其在指数部分,可以退化为高斯分布前面的系数,其对于我们研究这个高斯分布本身的均值和方差没有帮助,可以暂时忽略掉。
因此,我们对照正态分布的公式,可以写出这个分布的均值和方差如下所示:
\[\mu=-\frac{B}{2A}\] \[\sigma^2=\frac{1}{A}\]而在此之中,我们同样写出$A,B$的表达式如下所示:
\[A=\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}}\] \[B=-2(\frac{\sqrt{\alpha_t}x_t}{\beta_t}+\frac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}})\]然后,我们对$\mu$和$\sigma$进行简单的推导,如下所示:
\[\begin {aligned} \sigma^2&=\frac{1}{A} \\\ &=\frac{1}{\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}}} \\\ &=\frac{\beta_t(1-\bar\alpha_{t-1})}{\beta_t+(1-\bar\alpha_{t-1})\alpha_t} \\\ &=\beta_t\frac{1-\bar\alpha_{t-1}}{1-\alpha_t+\alpha_t-\bar\alpha_t} \\\ &=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t \end {aligned} \tag{12}\] \[\begin {aligned} \mu&=-\frac{B}{2A} \\\ &=(\frac{\sqrt{\alpha_t}x_t}{\beta_t}+\frac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}})\sigma^2 \\\ &=(\frac{\sqrt{\alpha_t}x_t}{\beta_t}+\frac{\sqrt{\bar\alpha_{t-1}}x_0}{1-\bar\alpha_{t-1}})\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t \\\ &=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_{t}}\sqrt{\alpha_t}x_t+\frac{\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t}}\beta_t{x_0} \end {aligned} \tag{13}\]对于式(12)(13),我们所期望的结果是获得仅仅和$x_t$相关的分布。我们可以看到,(12)表示的方差是一个确定的部分。对于(13)当中出现的$x_0$项,我们可以通过$\tilde{Z}$来写出$x_0$,即公式(8)。所以我们联立式(8)和式(13):
\[\begin{aligned} \mu&=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_{t}}\sqrt{\alpha_t}x_t+\frac{\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t}}\frac{\beta_t}{\sqrt{\bar\alpha_t}}(x_t-\sqrt{1-\bar\alpha_t}\tilde{Z}) \\\ &=\frac{x_t}{\sqrt{\alpha_t}}(\frac{\alpha_t-\bar\alpha_t}{1-\bar\alpha_t}+\frac{\beta_t}{1-\bar\alpha_t})-\frac{\tilde{Z}}{\sqrt{\alpha_t}}\frac{\beta_t}{\sqrt{1-\bar\alpha_t}} \\\ &=\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\tilde{Z}) \end{aligned} \tag{14}\]算到这里,我们需要回顾一下初心,我们想求得的是$q(x_{t-1}\mid{x_t})$这个分布。我们首先通过贝叶斯公式进行转换,然后求得了我们想要的分布的均值(14)和方差(12),这里我们给出最终的结论。
\[q(x_{t-1}\mid{x_t})\sim{N(\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\tilde{Z}),\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t)}\]而根据重采样技术,我们想要求得的$x_{t-1}$就可以写为:
\[x_{t-1}=\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\tilde{Z})+\sqrt{\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t}Z \tag{15}\]而在其中,我们有:
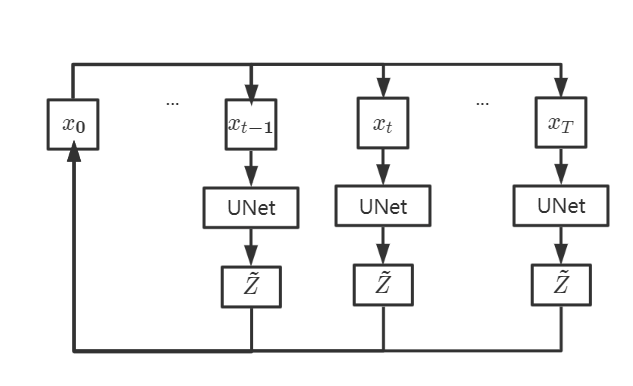
\[\tilde{Z}=UNet(x_t,t)\] \[Z\sim{N(0,\textbf{I})}\]经过比较冗杂的推导,我们得到了形如(15)这样的最终目标。最终我们来表示一下reverse的完整过程。
然后我们给出Diffusion Model当中原论文的算法部分,并且可以把它和我们的公式当中的每一项一一对应起来:
Diffusion Language Model
(先暂时归纳到这里,这个部分正在写)
(上面那个括号写于起码半个月前,没想到懒狗如我到现在具体数学课上太无聊才能继续写论文的内容)
首先要说明的是,时至今日,我仍然看不太懂这个论文的代码。
从连续域到离散域
如我们前文所讲的Diffusion Model,我们能够看到,通俗来讲,我们的扩散模型实际上是在一个向量当中逐步添加高斯噪声,最终得到一个趋于完全高斯噪声的向量。而在解码过程当中,我们则是尝试对一个高斯噪声逐步进行去噪,最终产生我们想要的向量(当然这里,无论他是什么样的形式,一个图像或是一个文本)。而这些过程实际上是针对连续域而言:我们可以很自然的将图像视作一个向量,但是其实文本的内容是离散的。
因此我们想要将Diffusion Model应用于文本生成领域,我们需要能够联系起离散域和连续域的工具。文中给出的方法是定义Embedding和Rounding方法,来实现从离散域到连续域和从连续域到离散域之间的转换。
End to End Training
为了将连续扩散模型应用于离散文本,我们定义了一个嵌入函数$EMB(w_i)$,给出这样的定义$EMB(w)=[EMB(w_1),EMB(w_2),…,EMB(w_n)]\in{R^{nd}}$
在这里,作者貌似尝试使用预训练的Embedding或者随机的高斯分布Embedding,但是发现没有重新End2End训练出来效果要好。
因此,在将扩散模型应用在离散文本当中时,我们添加了一个正向的马尔可夫变换和一个反向的rounding方法。其中正向的Embedding被定义为$q_{\phi}(x_0\mid{w})=\mathcal{N}(EMB(w),\sigma_{0}I)$,反向的Rounding被定义为$p_\theta(w\mid{x_0})=\prod_{i=1}^{n}p_\theta(w_i\mid{x_i}),p_\theta(w_i\mid{x_i})是一个softmax分布$。因此,我们可以将训练函数优化为如下所示:
Reducing Rounding Error
我们前文给出了Embedding和Rounding方法,其中,对于Rounding过程,我们想要的是将向量$x_0$还原为文本$w$,但是我们发现,去噪的步骤往往难以直接给出对应到某个单词的$x_0$,我们需要在这个步骤当中做出额外的处理。
首先给出的方法的原理是这样的,由于我们在目标函数当中对于$x_0$的结构建模不够,我们在普通的Diffusion Model当中使用UNet去预测噪声,而我们应该更重视$x_0$的建模,因此新的模型当中直接给出了有关$x_0$的优化。即给出从:
\[\mathcal{L}_{simple}(x_0)=\sum_{t=1}^{T}\mathbb{E}_{x_t}\|\mu_{\theta}(x_t,t)-\hat{\mu}(x_t,x_0)\|^2\]到
\[\mathcal{L}_{x_0-simple}^{e2e}(x_0)=\sum_{t=1}^{T}\mathbb{E}_{x_t}\|f_{\theta}(x_t,t)-x_0\|^2\]来迫使我们的模型直接去预测$x_0$,从而我们的模型能够明确$x_0$需要精准的位于一个词嵌入的中心。
重新制定目标函数确实有利于模型的训练,但是论文也给出了一个“clamping trick”。在标准的解码过程中,我们实际上是从$x_t$逐步去除高斯噪声,即$x_{t-1}=\sqrt{\bar\alpha}f_\theta(x_t,t)+\sqrt{1-\bar\alpha}\epsilon$,而我们现在给出clamping方法,其实是给出这样的去噪过程:$x_{t-1}=\sqrt{\bar\alpha}Clamp(f_\theta(x_t,t))+\sqrt{1-\bar\alpha}\epsilon$,强迫每一步都将预测的向量集中在词嵌入当中,减少舍入误差。
总得来说,文本的内容就是在每个反向重建的过程当中应用clamping(夹紧)技巧,使得我们的向量逼近于某一个词向量。根据我们的直觉,其实在$t$比较接近$T$的时候,应用夹紧技巧在直觉上来讲是次优的,这点作者在注释当中也有说明,但是作者也说明了,根据经验,即使对于每一步都应用这样的方法也问题不大(猜想是根据实验结果来判断的)。
Contollable Text Generation
作者受到前文的贝叶斯公式的启发,其应用了类似贝叶斯公式的方法。作者设计了一个即插即用的方法来完成可控的文本生成,对于解码过程当中的每一步,我们将文本生成当中“可控”的部分看作$c$,每步可控扩散的过程为$p(x_{t-1}\mid{x_t,c})\propto{p(x_{t-1}\mid{x_t})}\cdot{p(c\mid{x_{t-1},x_t})}$。由于之前其他文章的条件独立性假设,我们可以简化$p(c\mid{x_{t-1},x_t})=p(c\mid{x_{t-1}})$。
我们可以得到梯度下降的公式如下所示:
\[\nabla_{x_{t-1}}\log{p(x_{t-1}\mid{x_t,c})}=\nabla_{x_{t-1}}\log{p(x_{t-1}\mid{x_t})}+\nabla_{x_{t-1}}\log{p(c\mid{x_{t-1}})}\]而对于以上等式右边的两个加数,前者由Diffusion-LM参数化,后者由神经网络分类器参数化,因此两者都是可微的。
类似于图像生成当中的工作,我们在扩散隐变量上训练分类器,并且在隐空间当中应用梯度更新的技巧,从而来引导控制生成。
为了提升文本的质量以及加快解码速度(确实还是慢的不行),我们引入了关键的修改:流畅性正则化以及多重梯度步骤。
Fluency Regularization
虽然了解甚少,但是看起来,它是将梯度下降的目标函数更新为\(\lambda\log{p(x_{t-1}\mid{x_t})}+\log{p(c\mid{x_{t-1}})}\)其中$\lambda$是一个超参数,来平衡流畅性(前者)和控制性(后者)。
文中还提到这似乎是一种流行的文本生成技术。
Multiple Gradient Steps
为了提升控制质量,作者为每个扩散步骤使用多个梯度步骤,并且减少了扩散的总步骤。
Minimum Bayes Risk Decoding
应用了一个最小贝叶斯风险解码的trick,通过一个动态函数(其实是BLEU),希望解码出的句子尽可能地相似。(虽然不懂,但是好像懂了)